Maths KIRF
Key Instant Recall Facts
Multiplication Facts and Hints
Every multiplication has a twin, which may be easier to remember.
For example if you forget 8×5, you might remember 5×8. This way, you only have to remember half the table.
|
to multiply by |
Trick |
|---|---|
|
2
|
add the number to itself (example 2×9 = 9+9) |
|
5
|
the last digit goes 5, 0, 5, 0, ... |
|
|
is always half of 10× (Example: 5x6 = half of 10x6 = half of 60 = 30) |
|
|
is half the number times 10 (Example: 5x6 = 10x3 = 30) |
|
6
|
when you multiply 6 by an even number, they both end in the same digit. Example: 6×2=12, 6×4=24, 6×6=36, etc |
|
9
|
the last digit goes 9, 8, 7, 6, ... |
| is 10× the number minus the number. Example: 9×6 = 10×6−6 = 60−6 = 54 | |
|
|
when you add the answer's digits together, you get 9.
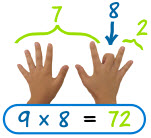
When learning the 9 times table, remember that the number in the 10s column will be one less than the number they are multiplying 9 by. For example, 8 x 9 will have a 7 in the tens column as it is 1 less than the 8 and the answer is a number bond to 9. Therefore 8 x 9 is 72 because 7 + 2 = 9. |
|
10
|
put a zero after it |
|
11
|
up to 9x11: just repeat the digit (Example: 4x11 = 44) |
| for 10x11 to 18x11: write the sum of the digits between the digits Example: 15x11 = 1(1+5)5 = 165 Note: this works for any two-digit number, but when the sum of the digits is more than 9, we need to"carry the one". Example: 75x11 = 7(7+5)5 = 7(12)5 = 825. |
|
|
12
|
is 10× plus 2× |
Remembering Squares Can Help
This may not work for you, but it worked for me. I like remembering the squares (where you multiply a number by itself):
| 1×1=1 | 2×2=4 | 3×3=9 | 4×4=16 | 5×5=25 | 6×6=36 |
| 7×7=49 | 8×8=64 | 9×9=81 | 10×10=100 | 11×11=121 | 12×12=144 |
And this gives us one more trick. When the numbers we are multiplying are separated by 2 (example 7 and 5), then multiply the number in the middle by itself and subtract one. See this:
| 5×5 = 25 is just one bigger than 6×4 = 24 |
| 6×6 = 36 is just one bigger than 7×5 = 35 |
| 7×7 = 49 is just one bigger than 8×6 = 48 |
| 8×8 = 64 is just one bigger than 9×7 = 63 |
| etc ... |